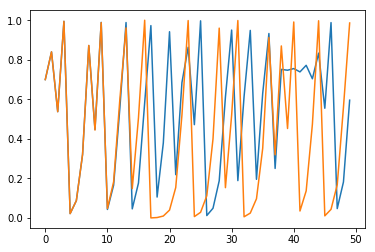
Illustration of the logistic map, $x_{n+1} = f(x_n) = r \cdot x_n \cdot (1 - x_n)$
At $r_1=3$, a stable period $2^1=2$ orbit is born. At $r_2=3.449$ a stable period $2^2=4$ orbit is born. As $r$ continues to increase, the period doublings continue until $r_{\infty} \approx 3.56995$ after which chaotic dynamics begin to occur, interspersed with periodic windows.
The Feigeinbaum constant $\delta=4.6692\dots$ is the ratio of subsequent differences between the values of $r_n$ at which the period doubles, as $n$ approaches infinity.
import numpy as np
import matplotlib.pyplot as plt
import pylab
def f(x, R):
return R * x * (1 - x)
def run_simulation(R, x_0, num_steps):
x_list = np.zeros(num_steps)
x_list[0] = x_0
for t in range(num_steps-1):
x_list[t+1] = f(x_list[t], R)
return x_list
def plot_two(x_list, y_list):
plt.plot(x_list)
plt.plot(y_list)
x_list = run_simulation(R=4, x_0=0.7, num_steps=50)
y_list = run_simulation(R=4, x_0=0.70001, num_steps=50)
plot_two(x_list, y_list)
